Ein Ruderboot fährt dieselbe Strecke hin und zurück: Braucht es mit Strömung länger oder hebt sich der Effekt auf? Vermutlich hat sich jeder Ruderer diese Frage schon einmal gestellt: Hat die Strömung nun Einfluss auf die Zeit die wir auf dem Wasser verbringen?

Mit ein wenig Nachdenken ist die Antwort gar nicht so schwer. Aber wenn ich genauer darüber nachdenke, ist es schon wieder gar nicht so einfach. Aber der Reihe nach…

Die (un)heile Welt

Die anschauliche Lösung

Beginnen wir mit einer einfachen Überlegung: Nehmen wir an, die Strömung beschleunigt unser Ruderboot mit dem Strom in demselben Maß wie sie uns gegen den Strom verzögert. Betrachtet man nur die Bootsgeschwindigkeit, hebt sich der Effekt also auf.

Aber: Da wir gegen den Strom langsamer sind, brauchen wir für dieselbe Distanz länger. Also sind wir länger dem Nachteil als dem Vorteil ausgesetzt. Das heißt: wir brauchen länger!

Rechnen wir ein Beispiel

Nehmen wir an, unser Ruderboot fährt ohne Strömung eine Geschwindigkeit von 10 km/h. Nehmen wird nun eine Strömung von 4 km/h an. Sagen wir, wir rudern je 5 km hin und zurück. Also 5 km gegen und anschließend 5 km mit dem Strom.

Zusammengefasst: $$\begin{eqnarray} \text{Annahme: }\text{Bootsgeschwindigkeit } v_{Boot} &=& 10 km/h\newline \text{Annahme: }\text{Strömungsgeschwindigkeit } v_{Strom} &=& 4 km/h\newline \text{Annahme: }\text{einfache Strecke } s &=& 5 km\newline \text{gesucht: }\text{benötigte Zeit gegen den Strom } t_{Berg}(s)\newline \text{gesucht: }\text{benötigte Zeit mit den Strom } t_{Tal}(s)\newline \text{gesucht: }\text{benötigte Zeit hin und zurück } t_{gesamt}(s)\newline \end{eqnarray}$$

Rechnen wir das Beispiel durch: $$\begin{eqnarray} t_{Berg}(s) &=& \frac{5 km} {10 km/h - 4 km/h} = 50 min\newline t_{Tal}(s) &=& \frac{5 km} {10 km/h + 4 km/h} \approx 21,43 min\newline t_{gesamt} &=& t_{Berg} + t_{Berg} \approx 71,43 min \end{eqnarray}$$

Würden wir im Vergleich die gesamte Strecke ohne Strömung mit 10 km/h bewältigen: $$\begin{eqnarray} t_{strömungslos}(s) &=& \frac{2 \cdot 5 km} {10 km/h} = 1 h \end{eqnarray}$$

D.h. mit Strömung sind wir deutlich länger unterwegs - 11 Minuten in unserem Beispiel.

Ruder wissen: Die Strömung nimmt zum Ufer ab

Doch Ruderer wissen: die Strömung nimmt zum Ufer hin ab. Daher fahren Talfahrer in der Flussmitte, Bergfahrer am Ufer. Zur Wahl des Ruderkurses bei Strömung gibt es diverse Erläuterungen, wie z.B. von den Kollegen von rowperfect : Strömende Gewässer – Rudern und Steuern am Fluss .

Jetzt stellt sich die Frage, wie groß dieser Unterschied ist und ob wir dadurch bei Strömung vielleicht doch schneller sind.

Gerinnehydraulik

Ich bin sicher kein Experte der Hydrodynamik. Dennoch habe ich versucht, mich etwas schlauer zu machen.

Scheinbar bewegen wir uns im Umfeld der Gerinnehydraulik . Dort findet man diverse Fließformeln . Mit deren Hilfe kann man die Fließ-/Strömungsgeschwindigkeit in Abhängigkeit des hydraulischen Radius und des Gefälles berechnen. Hinzu kommt jeweils ein Faktor zur Grundbeschaffenheit.

Bei meiner Recherche bin ich auf das frei verfügbare Buch »Einführung in die Gerinnehydraulik« von Gerhard H. Jirka und Cornelia Lang¹ gestoßen.

Darin heißt es:

In gegliederten Verbundprofilen [… ] mit zwei oder mehreren Querschnittsflächen mit oft stark unterschiedlichen Wassertiefen bzw. Rauheitsverhältnissen wird der Gesamtabfluss durch die Summe der Teilabflüsse ermittelt.

D.h. wir können also (zumindest näherungsweise) die Fließgeschwindigkeit für Ufernähe und Flussmitte getrennt berechnen, als würden wir zwei Flüsse unterschiedlicher Tiefe betrachten.

Die Fließgeschwindigkeit kann mit der Fließformel nach Gauckler-Manning-Strickler berechnet werden. Praktischerweise gibt es hierzu einen Online-Rechner auf der Homepage von Gabriel Strommer .

Beispiel Nahe

Rechnen wir also ein Beispiel:

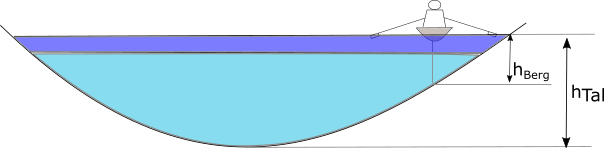
Ich rudere meist auf der Nahe in Bad Kreuznach. Die Tiefe schätze ich auf 1,2 m. Nehmen wir an, bei der Fahrt unter Land ist das Wasser 45 cm tief. Wenn wir nun die beiden Tiefen unabhängig voneinander betrachten wollen, nehmen wir dafür jeweils eine Breite der Rinne von 3 m an. Laut Wikipedia hat die Nahe ein Sohlgefälle von 3 ‰ - das nehmen wir auch für mein Teilstück an. Nach dem Online-Rechner ergibt sich eine Fließgeschwindigkeit in der Flussmitte von 5,4 km/h und 3,42 km/h in Ufernähe.

$$\begin{eqnarray} \text{Annahme: }\text{Flusstiefe in Flussmitte } h_{Tal} &=& 1,2 m\newline \text{Annahme: }\text{Flusstiefe in Ufernähe } h_{Berg} &=& 0,45 m\newline \text{Annahme: }\text{Breite der angenommenen Rinne } b &=& 3 m\newline \text{Annahme: }\text{Gefälle } I &=& 0,3\% \newline \text{Annahme: }\text{Rauheit / Strickler-Beiwert } k_{St}(s) &=& 35 m^{1/3}/s \newline \text{Fließgeschwindigkeit in Flussmitte } v_{Strom-Tal}(s) &=& 1,5 m/s = 5,4 km/h \newline \text{Fließgeschwindigkeit in Ufernähe } v_{Strom-Berg}(s) &=& 0,95 m/s = 3,42 km/h \newline \end{eqnarray}$$

Damit ergibt sich $$\begin{eqnarray} t_{Berg}(s) &=& \frac{5 km} {10 km/h - 3,42 km/h} \approx 45,59 min\newline t_{Tal}(s) &=& \frac{5 km} {10 km/h + 5,4 km/h} \approx 19,48 min\newline t_{gesamt} &=& t_{Berg} + t_{Berg} \approx 65,07 min \end{eqnarray}$$

Damit hat sich bestätigt, dass Ruderer die Strömung besser nutzen können - wir haben 5 min „herausgeholt«. Aber wir sind noch immer langsamer mit als ohne Strömung.

Steigender Pegel

Was ändert sich an unserem Beispiel, wenn der Pegel steigt?

Bei der Fahrt mit dem Strom haben wir eine entsprechend größere Wassertiefe und damit auch eine größere Fließgeschwindigkeit auf unserer Seite.

Der Einfluss auf die Fahrt gegen den Strom hängt jedoch stark von der Uferbeschaffenheit ab. Ist das Ufer steil oder hindert uns der Bewuchs, haben wir auch bei der Bergfahrt eine größere Wassertiefe und damit mehr Strömung.

Steigt das Ufer jedoch sanft an und hindert uns kein Bewuchs, können wir idealerweise mit derselben Wassertiefe wie vorher gegen den Strom rudern. In diesem Fall würde der steigende Pegel also ausschließlich für einen größeren Vorteil im Strom sorgen. Damit kann uns die Strömung schneller machen.

Echte Daten und echte Erfahrung

Wenn ich rudere, notiere ich mir meine Durchschnittsgeschwindigkeit und den Flusspegel. In der folgenden Grafik habe ich nun die Durchschnittsgeschwindigkeit gegen den Pegel aufgetragen. Dabei gilt:

• Alle Fahrten waren auf meiner Haustrecke.
• Alle Fahrten hatten in etwa die gleiche Distanz.
• Alle Fahrten waren im Einer: Rotenfels ist ein einfacher Renneiner. Libertas ist mein LiteRIVER.

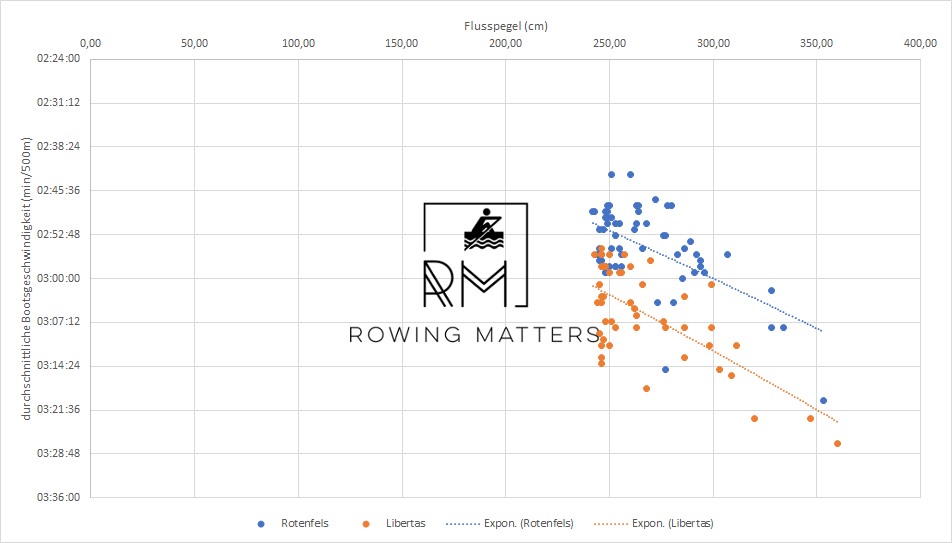
Man erkennt, dass meine Geschwindigkeit nach Tageslaune und -form variiert. Aber neben den Fahrten habe ich auch eine exponentielle Trendlinie pro Boot aufgetragen. Diese zeigt eine annähernd liniere Korrelation von durchschnittlicher Bootsgeschwindigkeit und Flusspegel bzw. Strömung.

Fazit

Es mag Bedingungen geben, unter denen ein erfahrener Ruderer/Steuermann durch geschickte Wahl des Kurses bei Strömung schneller ist. Es ist es aber auch so, dass wir Ruderer nie so richtig dicht ans Ufer kommen, da wir ja noch ca. 3 m lange Ruder bei uns haben. Außerdem kostet es viel Aufmerksamkeit, sehr dicht unter Land zu fahren.

Meiner Erfahrung nach, wird man mit zunehmender Strömung langsamer. Gestützt wird dies durch die Beispielrechnungen und meine gesammelten Daten. Gleichzeitig sagt meine Erfahrung aber auch, dass die Wahl des Kurses unter Land oftmals deutlich unterschätzt wird. Bei starker Strömung kann der Unterschied beträchtlich sein. Ich erinnere an eine Fahrt gegen den Rhein, bei der wir im Vierer kaum einen locker paddelnden Kanuten überholen konnten.

Disclaimer: Offensichtlich sind die Rechnungen stark vereinfacht. Ich bin von einer gleichförmigen Bewegung ohne Anfahren und Stoppen ausgegangen, das Abtreiben beim Wenden habe ich nicht beachtet. Die Bootsform hat sicher auch einen Einfluss. Und und und…

Weitere Artikel zur Geschwindigkeit von Ruderbooten

• Überholmanöver unter Ruderbooten in strömendem Gewässer (31.08.2021)
• Weshalb es bei Ruderbooten auf die Länge ankommt (15.12.2020)

Erwin Doorn